1079. Removing
the letters
You are given two
words (each word consists of upper-case English letters). Delete some letters
from each word so that the resulting words become equal.
Find the maximum
possible length of the resulting word.
Input. Each test case consists of a single line,
containing two words separated by a space. The length of each of these words is
between 1 and 200. There are no more than 10 test
cases.
Output. For each test case output the maximum length
of a resulting word (the length of the longest word that can be created from
both words by removing some letters).
If two words have
no letters in common, print 0.
|
Sample
input |
Sample
output |
|
AAABBB ABABAB AXYAAZ CXCYCZC ABCDE EDCBA |
4 3 1 |
SOLUTION
dynamic programming - LCS
Algorithm analysis
The answer to
the problem is the length of the longest common subsequence (LCS) of input sequences of uppercase
Latin letters.
Let f(i, j)
be the longest common
subsequence of
sequences x1x2…xi and y1y2…yj.
If xi ¹ yj, then find LCS between x1x2…xi-1 and y1y2…yj,
and also
between x1x2…xi and y1y2…yj-1. Return the largest of them:
f(i, j) = max( f(i,
j – 1), f(i – 1, j) )
If xi = yj,
then find LCS between x1x2…xi-1 and y1y2…yj-1:
f(i, j) = 1 + f(i –
1, j – 1)
The values f(i, j)
will be
stored in array m[0.. SIZE, 0.. SIZE], where m[0][i] = m[i][0] = 0. Since the length of
words is no more than 200 characters then assign SIZE = 201.
Each next line
of array m[i][j] is calculated through the previous one.
Therefore, to find the answer, it is enough to keep only two lines in memory.
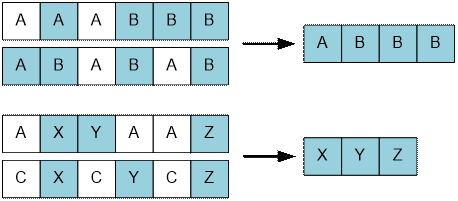
Example
Here is given the largest
common subsequences for samples.
Algorithm realization
Strings x and y contain input sequences, lenx
and leny are their lengths. Array m contains
the last two lines of dynamic computations.
#define SIZE 1001
string x, y;
int m[2][SIZE];
int lenx, leny;
Input data are processed till the end of
file. Read two input
sequences into strings x and y. We add a space before the strings, so that the sequences will start from the
first position. Store the positions of the last
characters in the strings in the variables lenx
and leny.
while (cin >> x >> y)
{
x = ' ' + x; lenx = x.size() - 1;
y = ' ' + y; leny = y.size() - 1;
Set array m to zero. Dynamically compute the values of f(i, j).
Initially, m[0][j] contains the
values f(0, j). Further, in m[1][j] we store the values of f(1, j). Since to calculate f(2, j) it is enough to have the values of two previous rows of array m,
then the values f(2, j) can be stored
in cells m[0][j], the values f(3, j) can be stored in cells m[1][j] and so on.
memset(m,0,sizeof(m));
for(i = 1; i <=
lenx; i++)
for(j = 1; j <=
leny; j++)
if (x[i] == y[j]) m[i % 2][j] = 1 + m[(i-1)%2][j-1];
else m[i % 2][j] = max(m[(i-1)%2][j],m[i%2][j-1]);
At the end of
the algorithm, the length of the longest common subsequence will be in the cell m[lenx%2][leny]. Print it.
cout << m[lenx % 2][leny] << endl;
}